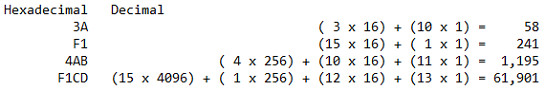Частина 6: Шістнадцяткова система числення
Для повного змісту змісту всіх уроків, будь ласка, натисніть нижче, оскільки це надасть вам короткий зміст кожного уроку, а також теми, які будуть розглянуті. https://github.com/mytechnotalent/Reverse-Engineering-Tutorial
Тепер, коли ми вже є майстрами двійкової системи числення, настав час розібратися з системою числення систем числення!
У двійковій системі ми дізналися, що кожна цифра представляє біт. Якщо об'єднати 8 бітів, отримаємо байт. Байт можна додатково розділити на верхні 4 біти та нижні 4 біти. Комбінація 4 бітів — це нібл. Оскільки 4 біти дають можливий діапазон від 0 до 15, з системою числення з основою 16 працювати простіше. Майте на увазі, що коли ми говоримо про основу 16, ми починаємо з 0, а отже, 0–15 — це 16 різних чисел.
Ця цікава система числення називається шістнадцятковою. Причина, чому ми використовуємо цю систему числення, полягає в тому, що в асемблері x86 набагато простіше виражати двійкові числа в шістнадцятковій системі, ніж в будь-якій іншій системі числення.
Шістнадцяткова система числення схожа на всі інші системи числення, за винятком того, що в шістнадцятковій системі кожна колонка має значення, яке в 16 разів перевищує значення колонки праворуч від неї. Цікавим у шістнадцятковій системі є те, що ми маємо не тільки 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, а й A, B, C, D, E та F, а отже, 16 різних символів.
Давайте подивимося на просту таблицю, щоб побачити, як шістнадцяткова система порівнюється з десятковою.
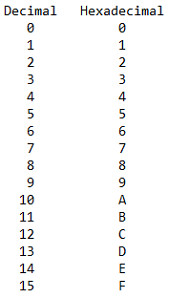
Добре, я бачу, як дим виходить з ваших вух, але все гаразд! У десятковій системі все обчислюється в степені 10. Візьмемо число 42 і розглянемо його в десятковій системі:
2 x 10 ^ 0 = 2
4 x 10 ^ 1 = 40
Пам'ятайте, що 10 в степені 0 дорівнює 1, а 10 в степені 1 дорівнює 10, отже, 2 + 40 = 42.
Візьміть каву, ось і найцікавіше!
Якщо ми розуміємо, що десяткова система числення є системою числення з основою 10, ми можемо створити просту формулу, де b представляє основу. У цьому випадку b = 10.
(2 * b ^ 0) + (4 * b ^ 1)
(2 * 10 ^ 0) + (4 * 10 ^ 1) = 42
У двійковій системі числення 42 десяткове число дорівнює 0010 1010 двійкове число, як показано нижче:
0 x 2 ^ 0 = 0
1 x 2 ^ 1 = 2
0 x 2 ^ 2 = 0
1 x 2 ^ 3 = 8
0 x 2 ^ 4 = 0
1 x 2 ^ 5 = 32
0 x 2 ^ 6 = 0
0 x 2 ^ 7 = 0
0 + 2 + 0 + 8 + 0 + 32 + 0 + 0 = 42 десяткове число
У шістнадцятковій системі все обчислюється в степені 16. Тому 42 в десятковій системі дорівнює 2A в шістнадцятковій системі:
10 * 16 ^ 0 = 10
2 * 16 ^ 1 = 32
10 + 32 = 42 десяткова система => 2A шістнадцяткова система
Це те саме, що сказати:
10 * 1 = 10
2 * 16 = 32
10 + 32 = 42 десяткова система => 2A шістнадцяткова система
Майте на увазі, що 10 десяткова система дорівнює A шістнадцяткова система, а 2 десяткова система дорівнює 2 шістнадцяткова система. У нашій формулі вище, коли ми маємо справу з A, B, C, D, E або F, нам потрібно перетворити їх у їх десяткову еквівалентну величину.
Візьмемо інший приклад шістнадцяткового числа F5. Це буде виглядати так:
5 x 16 ^ 0 = 5
15 x 16 ^ 1 = 240
5 + 240 = 245 десяткове => F5 шістнадцяткове
Давайте подивимося на таблицю перетворення двійкових чисел у шістнадцяткові:

Важливо розуміти, що кожне шістнадцяткове число має довжину 4 біти або називається ніблом. Це стане критично важливим, коли ми будемо здійснювати реверс-інжиніринг наших програм на C в асемблер.
Давайте подивимося на це з іншого боку. Давайте попрацюємо з декількома шістнадцятковими числами і перетворимо їх в десяткові:
Щоб ще раз підкреслити F1CD як просте перетворення:
D --- 13 x 1 = 13
C --- 12 x 16 = 192
1 --- 1 x 256 = 256
F --- 15 x 4096 = 61,440
13 + 192 + 256 + 61,440 = 61,901
Додавання в шістнадцятковій системі працює наступним чином. З цього моменту всі числа в шістнадцятковій системі будуть мати літеру «h» поруч із числом:

Інший приклад:
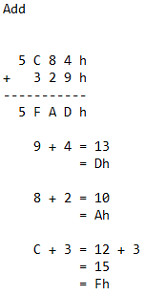
Останній приклад додавання такий:
Тепер зосередимося на відніманні:
Ви, мабуть, запитуєте себе, чому цей хлопець витрачає стільки часу на вивчення стількох різних способів навчання! Відповідь полягає в тому, що кожен з нас вчиться трохи по-різному. Я хотів показати кілька представлень шістнадцяткової системи в порівнянні з десятковою та двійковою, щоб допомогти скласти загальну картину.
Для подальшого просування вперед дуже важливо зрозуміти, що тут відбувається. Якщо у вас є питання, будь ласка, залишайте коментарі нижче, і я з радістю допоможу!
У наступному уроці ми обговоримо перемикачі, транзистори та пам'ять.